Elementary Graph Algorithms

Graphs can be used to model many types of relations and processes in physical, biological, social and information systems. In computer science, graphs are used to represent networks of communication, data organization, computational devices, the flow of computation, etc.
For instance, the link structure of a website can be represented by a directed graph, in which the vertices represent web pages and directed edges represent links from one page to another.

What are graph representation?

We have one graph like this:

Fig. 1. An undirected graph with 5 vertices and 7 edges

We have 2 ways to represent this graph:

Fig. 2. The adjacency-list and adjacency-matrix representations

What 's about directed graphs?

Fig. 3. A directed graph G with 6 vertices and 8 edges (left), An adjacency-list representation of G (center) and The adjacency-matrix representation of G (right)

Conception 

We set a graph G = (V, E). 

- The adjacency-list representation of G: 

 + Consists of  |V| arrays Adj, one for each vertex in V. 

 + For each edge u, the adjacency list Adj[u] contains all the vertices v which is adjacent to u (exists an edge (u, v)) 

 + The sum of the lengths of all the adjacency lists is:  

   . |E| if G is a directed graph, 

   . 2|E| if G is a undirected graph.

- The adjacency-matrix representation of G: 

 + Consists of a |V| x |V| matrix A = (a_ij):    

  a_ij =  . 1 if (i, j) in E              

          . 0 otherwise+ Symmetric matrix: A = A^T

Advantage and Disadvantage

Table 1. Advantage and disadvantage of 2 graph representations

	Adjacency-list representation	Adjacency-matrix representation
Advantage	- Using memory in proportion to the number edges => save a lot of memory if the adjacency matrix is sparse - It is fast to iterate over all edges	- The presentation is simpler, especially when graphs are reasonably small. - Quick to determine whether a given edge (u, v) is present in the graph. - Using only 1 bit per entry for unweighted graphs.
Disadvantage	- Slow to determine whether a given edge (u, v) is present in the graph.	- Using more memory - Slow to iterate over all edges

What are these representations used for?

- Adjacency-list representation: sparse graphs (|E| << |V|^2 ) 

- Adjacency-matrix representation: dense graphs (|E| ~ |V|^2)

There are 2 elementary graph algorithms as below. These algorithms is used for searching, identifying graph data structures.

Breadth-first search

What are applications of BFS?

• Find the shortest path from a vertex s to a vertex v in an unweighted graph.
• Find the length of such a path.
• Find out if a graph contains cycles.
• Construct a BFS tree/forest from a graph.

Pseudocode

Input: A graph Graph and a starting vertex root of Graph.
Output: All vertices reachable from root labeled as explored.
Breadth-First-Search(Graph, root):

     for each node n in Graph:            
         n.distance = INFINITY        
         n.parent = NIL
 
     create empty queue Q      
 
     root.distance = 0
     Q.enqueue(root)                      
 
     while Q is not empty:        
     
         current = Q.dequeue()
     
         for each node n that is adjacent to current:
             if n.distance == INFINITY:
                 n.distance = current.distance + 1
                 n.parent = current
                 Q.enqueue(n)

This is an simulation of BFS with source node: 1, want to find node 13:

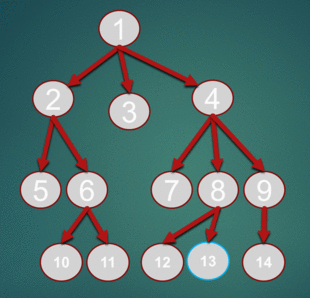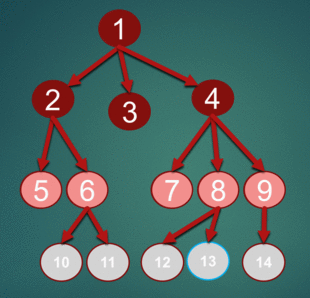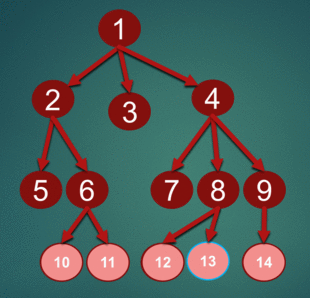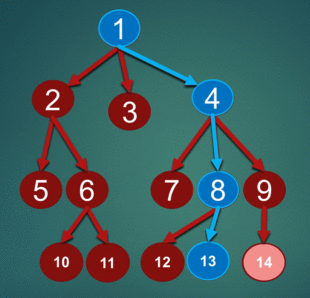
Implementation

??

Depth-first search

What are applications of BFS?

Pseudocode
Implementation

Finding Connected Components (Undirected Graph)

???
- Flood Fill - Labeling/Coloring the Connected Components
- Topological sort (Directed Acyclic Graph)
- Bipartite Graph Check
- Graph Edges Property Check via DFS Spanning Tree
- Finding Articulation Points and Bridges (Undirected Graph)
- Finding Strongly Connected Components (Directed Graph)