Dynamic Programming

created by Frank

1. What is Dynamic Programming?

• Dynamic programming solves problems by combining the solutions to subproblems. We typically apply dynamic programming to optimization problems. Such problems can have many possible solutions. Each solutions has a value, and we wish to find a solution with the optimal (maximum or minimum) value. 
• A sequence of 4 steps:

            -  Characterize the structure of an optimal solution
            -  Recursively define the value of an optimal solution
            -  Compute the value of an optimal solution, typically in a bottom-up fashion
            -  Construct an optimal solution from computed information

• Dynamic programming and recursive are different:

           -  Recursive starts at big problem which can be divided into many subprobems. We solve all those subproblems and each subproblem can be divided into many smaller subproblems. (top - down)
           -  Dynamic programming starts at resolving smallest subproblems (base problems). From that, we resolve bigger problems until finding the result for biggest problem. (original problem). (bottom-up)

Example: 
Fibonaci number

there are 2 methods to compute the fibonaci number bellow:

computing fibonaci number between recursive and dynamic programming

the disadvantage of recursive:

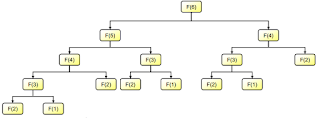F[6] computation

2. Some optimization problems

2.1 Rod cutting

Problem description: how to cut a rod into rods of smaller length in way that maximizes their total value. I buy a long steel rod and cut it into shorter rods to sell. 

Give a rod of length n inches and a table of prices pi for i= 1, 2, ..., n, determine the maximum revenue rn obtainable by cutting up the rod and selling the prices. If the price pn for a rod of length n is large enoughm, an optimal solution may require no cutting at all. 

A sample price table for rods. 

example: n = 4

the optimal strategy is part (c) - cutting the rod into 2 pieces of length 2 - which has total value 10.

the 8 possible ways of cutting up a rod of length 4

If an optimal solution cuts the rod into the k pieces, from some 1 <= k <= n,  then an optimal decomposition

n = i1 + i2 + ... + ik;

of the rod ino pieces of lengths i1, i2, i3, .., ik provides maximum corresponding revenue 

rn = pi1 + pi2 + .. + pik

the optimal result

More generally, we can frame the values rn for n >= 1 in terms of optimal revenues from shorter rods: 

the following simpler version of above equation:

bottom-up dynamic programming version of cut-rod problem 

C source code

#include <stdio.h>

int main()
{
 int p[11] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
 int r[11];
 int s[11];
 int i, j;
 int q;

 r[0] = 0;

 for(j = 1; j <= 10; j++)
 {
  q = -1; 
  for(i = 1; i <= j; i++)
  {
   if(q < p[i] + r[j-i])
   {
    q = p[i] + r[j-i];
    s[j] = i;
   }
  }
  r[j] = q;
 }

 for(i = 1; i <= 10; i++)
  printf("r[%d] = %d, s[%d] = %d\n", i, r[i], i, s[i]);

 return 0;
}

2.2 Matrix-chain multiplication

problem: give a sequence <A1, A2, .. , An> of matrices to be multiplied, and wish to compute the product:
                                           A1A2A3...An.
so how many are the minimum of scaler multiplications?

matrix-chain multiplication problem:
give a chain <A1, A2, .. An>  of n matrices, where i = 1, 2,.., n, matrix Ai has dimension

fully parenthesize the product A1A2...An in a way that minimizes the number of scalar multiplications.

Step 1: 

Call m[i, j] is the optimal value of product Ai...Aj. (i <= j). we must split the product between Ak and Ak+1 for some integer k in range i <= k <=j. That is, for some value of k, we first compute the matrices Ai..k and Ak+1..j and then multiply them together to produce the final product Ai..j. The cost this way is the cost of computing the matrix Ai..j plus the cost pf computing Ak+1...j , plus the cost of multiplying them together.

Step 2:

Step 3:

define s[i, j] to be a value of k at which we split the product AiAi+1...Aj in an optimal parenthesization.

The algorithm of matrix-chain 

Exampe: MATRIX-CHAIN-ORRDER for n = 6 and the following matrix demensions

and the below image shows the result of m and s array.

the m and s tables computed by Matrix-Chain-Order for n = 6

below is an example of computing m[2, 5]

The result is ((A1(A2A3))((A4A5)(A6)

the C source code

#include <stdio.h>
#include <limits.h> 

// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
int MatrixChainOrder(int p[], int n)
{
 
    /* For simplicity of the program, one extra row and one
       extra column are allocated in m[][].  0th row and 0th
       column of m[][] are not used */
    int m[n][n];
    int s[n][n];
 
    int i, j, k, L, q;
 
    /* m[i,j] = Minimum number of scalar multiplications needed
       to compute the matrix A[i]A[i+1]...A[j] = A[i..j] where
       dimension of A[i] is p[i-1] x p[i] */
 
    // cost is zero when multiplying one matrix.
    for (i=1; i< n; i++)
        m[i][i] = 0;
 
    // L is chain length.
    for (L=2; L < n; L++)
    {
        for (i=1; i< n-L+1; i++)
        {
            j = i+L-1;
            m[i][j] = INT_MAX;
            for (k=i; k<= j-1; k++)
            {
                // q = cost/scalar multiplications
                q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                if (q < m[i][j])
                {
                    m[i][j] = q;
                    s[i][j] = k;
                }
            }
            printf("m[%d][%d] %5d, s[%d][%d] %d \n", i, j, m[i][j], i, j, s[i][j]);
        }
    }
 
    return m[1][n-1];
}
 
int main()
{
    int i, j;
    int arr[] = {30, 35, 15, 5, 10, 20, 25};
    int arr_size = sizeof(arr)/sizeof(arr[0]);
 
    printf("Minimum number of multiplications is %d \n", MatrixChainOrder(arr, arr_size));
    
    return 0;
}

References

Thomas H. Conrmen, Charles E. Leisersion, Ronald L. Revest, Clifford Stein, Introduction to Algorithms, third edition